DeepSeek AI Releases DeepSeekMath-V2: The Open Weights Maths Model That Scored 118/120 on Putnam 2024
How can an AI system prove complex olympiad-level math problems in clear natural language while also verifying the correctness of its own reasoning? DeepSeek AI has addressed this challenge with the release of DeepSeekMath-V2, an open-weights large language model optimized for natural language theorem proving with self-verification. Built on DeepSeek-V3.2-Exp-Base, this 685B parameter mixture-of-experts model is available on Hugging Face under an Apache 2.0 license.
In testing, DeepSeekMath-V2 achieved gold-level scores on the 2025 International Olympiad in Mathematics (IMO) and 2024 Chinese Mathematical Olympiad (CMO). Most notably, it scored 118 out of 120 points on the 2024 Putnam Competition when using scaled test-time compute, surpassing the best human score of 90.
Why Final Answer Rewards Are Not Enough
Many recent math reasoning models rely on reinforcement learning that rewards only the final answer on benchmarks like the American Invitational Mathematics Examination (AIME) and Harvard-MIT Mathematics Tournament (HMMT). This approach quickly improved models from weak baselines to near-saturation on short-answer contests within a year. However, the DeepSeek research team identified two critical flaws in this method:
A correct numeric answer doesn’t guarantee correct reasoning—models might arrive at the right result through algebraic mistakes that cancel out.
Tasks like olympiad proofs and theorem proving require complete natural language arguments, which don’t have a single numeric answer, making standard answer-based rewards ineffective.
DeepSeekMath-V2 shifts focus from pure answer accuracy to proof quality. Instead of rewarding final results, the model evaluates whether a proof is complete and logically sound, using this assessment as its primary learning signal.
Training a Verifier Before the Generator
The core of DeepSeekMath-V2’s design is a “verifier-first” approach. The team trained a language model-based verifier capable of reading a problem and a candidate proof, then outputting a natural language analysis and a discrete quality score (0, 0.5, or 1) based on rigor and completeness.
Initial reinforcement learning data came from 17,503 proof-style problems crawled from olympiads, team selection tests, and post-2010 problems requiring explicit proofs—forming the base for cold-start RL. Candidate proofs were generated by a DeepSeek-V3.2 reasoning model prompted to iteratively refine solutions, creating detailed but imperfect proofs. Human experts labeled these proofs using the 0–1 rubric.
The verifier was trained with Group Relative Policy Optimization (GRPO), using two reward components:
– A format reward to ensure output followed a fixed template (including an analysis section and score box).
– A score reward to penalize differences between the verifier’s predicted score and the expert label.
This process produced a verifier capable of consistently grading olympiad-style proofs. For more details, see the DeepSeekMath-V2 paper.
Meta Verification to Control Hallucinated Critiques
Even a well-trained verifier can game rewards by outputting a correct score while inventing fake issues in its analysis—making explanations unreliable. To fix this, the team introduced a meta verifier that evaluates the faithfulness of the verifier’s analysis by checking:
– Restatement of the proof’s steps.
– Identification of real defects.
– Consistency between the narrative and final score.
Trained with GRPO (using its own format and score rewards), the meta verifier’s output (a meta quality score) is added as an extra reward for the base verifier. This means analyses with hallucinated problems get low meta scores even if the final proof score is correct. Experiments showed this increased the average meta-evaluated quality of analyses from 0.85 to 0.96 on a validation split while maintaining proof score accuracy.
Self-Verifying Proof Generator and Sequential Refinement
Once the verifier was robust, the team trained a proof generator that takes a problem and outputs both a solution and a self-analysis following the verifier’s rubric. The generator’s reward combines three signals:
1. The verifier’s score on the generated proof.
2. Agreement between the generator’s self-reported score and the verifier’s score.

3. The meta-verification score of the self-analysis.
Formally, the reward uses weights of α = 0.76 for proof score and β = 0.24 for self-analysis, multiplied by a format term to enforce structure. This encourages the generator to produce verifier-accepted proofs and be honest about flaws—claiming a flawed proof is perfect results in lost reward due to disagreement and low meta scores.
Leveraging the base model’s 128K token context limit, the team implemented sequential refinement for hard problems. If a single pass can’t fix all issues (due to context constraints), the system generates a proof and self-analysis, feeds them back as context, and asks the model to produce a revised proof addressing detected issues. This loop repeats until the context budget is exhausted. For more information, visit the DeepSeekMath-V2 repository.
Scaling Verification and Auto-Labeling
As the generator improved, it produced more complex proofs, making human labeling costly. To maintain fresh training data, the team created an automatic labeling pipeline using scaled verification. For each candidate proof:

1. Multiple independent verifier analyses are sampled.
2. Each analysis is evaluated by the meta verifier.
3. If high-quality analyses converge on the same serious issues, the proof is labeled incorrect.
4. If no valid issues survive meta-checking, the proof is labeled correct.
This pipeline replaced human labels in final training iterations, with spot checks confirming strong agreement with experts.

Competition and Benchmark Results
DeepSeekMath-V2 was evaluated across multiple benchmarks, with standout results:
Internal CNML Set: On 91 problems covering algebra, geometry, number theory, combinatorics, and inequalities, DeepSeekMath-V2 achieved the highest mean proof score compared to Gemini 2.5 Pro and GPT-5 Thinking High (as measured by its verifier).
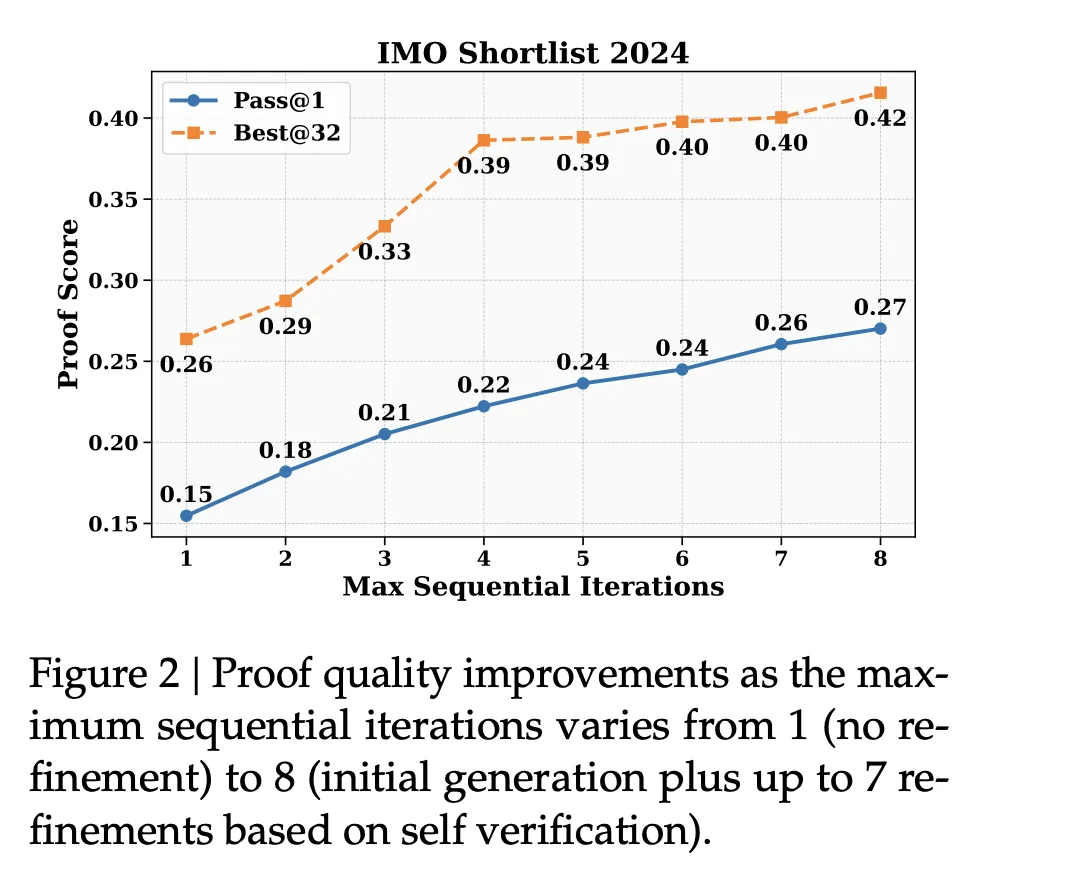
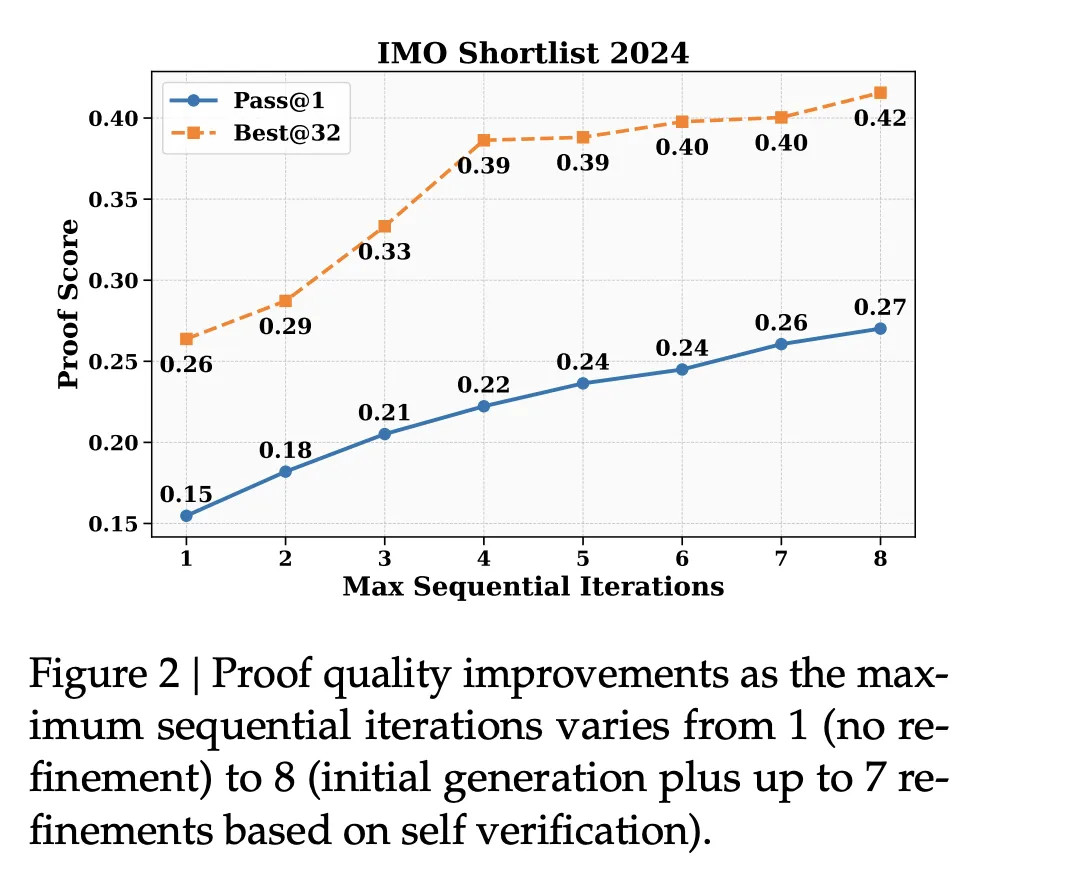
IMO Shortlist 2024: Sequential refinement with self-verification improved both “pass at 1” and “best of 32” quality metrics as the number of refinement iterations increased.
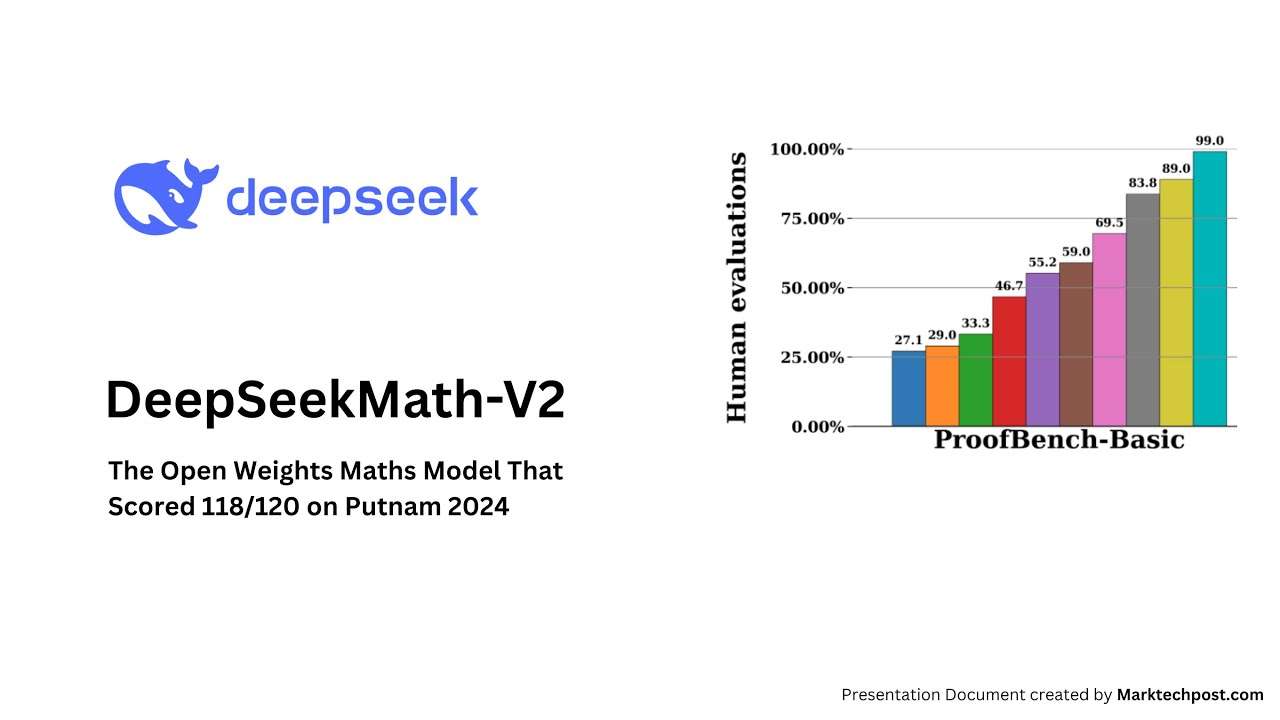
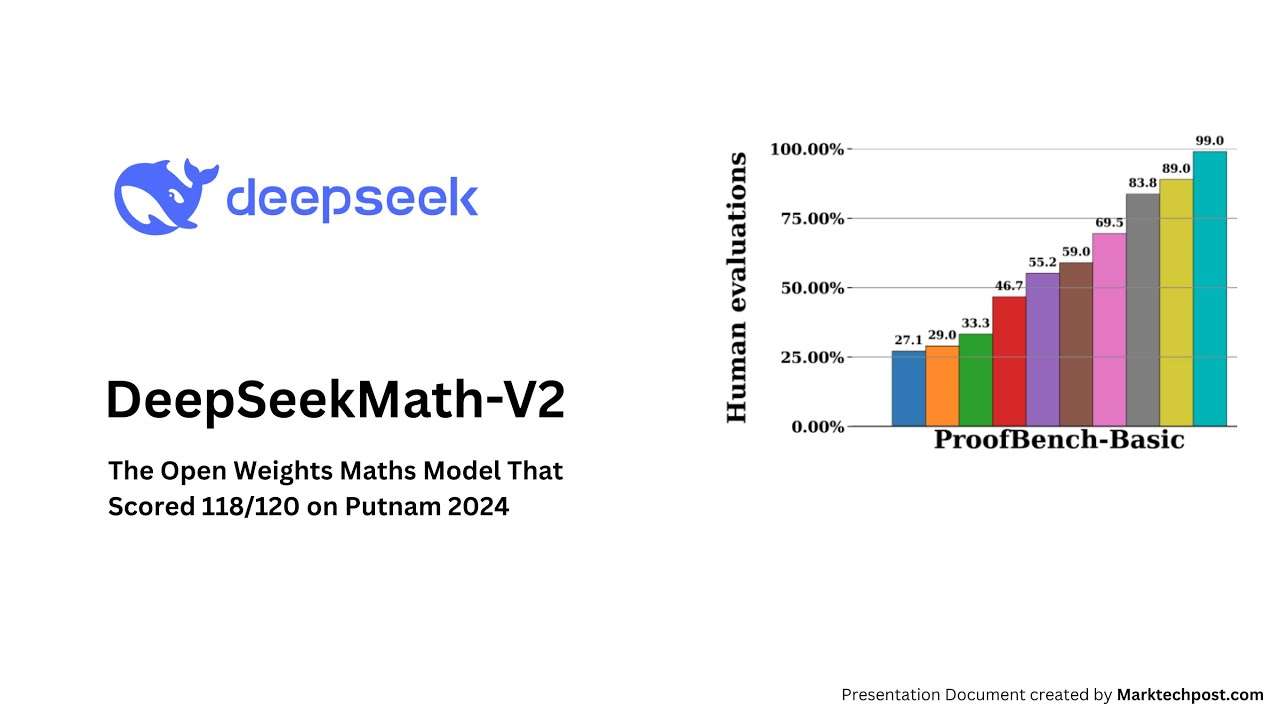
IMO ProofBench: Expert evaluations showed DeepSeekMath-V2 outperformed DeepMind’s DeepThink IMO Gold on the Basic subset and remained competitive on the Advanced subset, while outperforming other large models.

Full Competitions:
2025 IMO: Solved 5 of 6 problems (gold medal level).
2024 CMO: Solved 4 problems fully and earned partial credit on 1 (gold medal level).
2024 Putnam: Solved 11 of 12 problems completely (with minor errors on the 12th), resulting in a 118/120 score—surpassing the best human score of 90.
For detailed results, refer to the DeepSeekMath-V2 paper.

Key Takeaways
Model Overview: DeepSeekMath-V2 is a 685B parameter model built on DeepSeek-V3.2-Exp-Base, designed for natural language theorem proving with self-verification. It’s available as open weights under an Apache 2.0 license.
Verifier-First Design: The model uses a GRPO-trained verifier and meta verifier to score proofs for rigor (not just final answers), addressing the gap between correct answers and correct reasoning.
Generator Training: A proof generator is trained against these verifiers, with rewards combining proof quality, self-evaluation agreement, and analysis faithfulness. Sequential refinement allows iterative proof repair within the 128K context limit.
Performance: With scaled test-time compute, DeepSeekMath-V2 achieved gold-level performance on the 2025 IMO and 2024 CMO, plus a near-perfect 118/120 score on the 2024 Putnam—surpassing the best human score.




